5 Modeling
Chapter 5 of the Dynamic Learning Maps® (DLM®) Alternate Assessment System 2014–2015 Technical Manual—Year-End Model (Dynamic Learning Maps Consortium, 2016b) describes the basic psychometric model that underlies the DLM assessment system, while the 2015–2016 Technical Manual Update—Year-End Model (Dynamic Learning Maps Consortium, 2017b) provides a complete, detailed description of the process used to estimate item and student parameters from student assessment data. This chapter provides a high-level summary of the model used to calibrate and score assessments, along with a summary of updated modeling evidence from the 2019–2020 administration year.
For a complete description of the psychometric model used to calibrate and score the DLM assessments, including the psychometric background, the structure of the assessment system, suitability for diagnostic modeling, and a detailed summary of the procedures used to calibrate and score DLM assessments, see the 2015–2016 Technical Manual Update—Year-End Model (Dynamic Learning Maps Consortium, 2017b).
5.1 Overview of the Psychometric Model
Learning map models, which are networks of sequenced learning targets, are at the core of the DLM assessments in English language arts (ELA) and mathematics. Because of the underlying map structure and the goal of providing more fine-grained information beyond a single raw or scale score value when reporting student results, the assessment system provides a profile of skill mastery to summarize student performance. This profile is created using latent class analysis, a form of diagnostic classification modeling, to provide information about student mastery of multiple skills measured by the assessment. Results are reported for each alternate content standard, called an Essential Element (EE), at the five levels of complexity for which assessments are available: Initial Precursor, Distal Precursor, Proximal Precursor, Target, and Successor.
Simultaneous calibration of all linkage levels within an EE is not currently possible because of the administration design, in which overlapping data from students taking testlets at multiple levels within an EE is uncommon. Instead, each linkage level was calibrated separately for each EE using separate latent class analyses. Also, because items were developed to meet a precise cognitive specification, all master and non-master probability parameters for items measuring a linkage level were assumed to be equal. That is, all items were assumed to be fungible, or exchangeable, within a linkage level.
A description of the DLM scoring model for the 2019–2020 administration follows. Using latent class analysis, a probability of mastery was calculated on a scale from 0 to 1 for each linkage level within each EE. Each linkage level within each EE was considered the latent variable to be measured. Students were then classified into one of two classes for each linkage level of each EE: master or non-master. As described in Chapter 6 of the 2014–2015 Technical Manual—Year-End Model (Dynamic Learning Maps Consortium, 2016b), a posterior probability of at least .80 was required for mastery classification. Consistent with the assumption of item fungibility, a single set of probabilities of masters and non-masters providing a correct response was estimated for all items within a linkage level. Finally, a structural parameter, which is the proportion of masters for the linkage level (i.e., the analogous map parameter), was also estimated. In total, three parameters per linkage level are specified in the DLM scoring model: a fungible probability for non-masters, a fungible probability for masters, and the proportion of masters.
Following calibration, students’ results for each linkage level were combined to determine the highest linkage level mastered for each EE. Although the connections between linkage levels were not modeled empirically, they were used in the scoring procedures. In particular, if the latent class analysis determined a student had mastered a given linkage level within an EE, then the student was assumed to have mastered all lower levels within that EE.
In addition to the calculated posterior probability of mastery, students could be assigned mastery of linkage levels within an EE in two other ways: correctly answering 80% of all items administered at the linkage level or through the two-down scoring rule. The two-down scoring rule was implemented to guard against students assessed at the highest linkage levels being overly penalized for incorrect responses. When a student tested at more than one linkage level for the EE and did not demonstrate mastery at any level, the two-down rule was applied according to the lowest linkage level tested.
5.2 Calibrated Parameters
As stated in the previous section, the comparable item parameters for diagnostic assessments are the conditional probabilities of masters and non-masters providing a correct response to the item. Because of the assumption of fungibility, parameters are calculated for each of the 860 linkage levels across ELA and mathematics (5 linkage levels \(\times\) 172 EEs). Parameters include a conditional probability of non-masters providing a correct response and a conditional probability of masters providing a correct response. Across all linkage levels, the conditional probability that masters will provide a correct response is generally expected to be high, while it is expected to be low for non-masters. In addition to the item parameters, the psychometric model also includes a structural parameter, which defines the base rate of mastery for each linkage level. A summary of the operational parameters used to score the 2019–2020 assessment is provided in the following sections.
5.2.1 Probability of Masters Providing Correct Response
When items measuring each linkage level function as expected, students who have mastered the linkage level have a high probability of providing a correct response to items measuring the linkage level. Using the 2019–2020 operational calibration, Figure 5.1 depicts the conditional probability of masters providing a correct response to items measuring each of the 860 linkage levels. Because the point of maximum uncertainty is .50, masters should have a greater than 50% chance of providing a correct response. The results in Figure 5.1 demonstrate that the vast majority of linkage levels (n = 838, 97%) performed as expected. Additionally, 93% of linkage levels (n = 801) had a conditional probability of masters providing a correct response over .60. Only a few linkage levels (n = 9, 1%) had a conditional probability of masters providing a correct response less than .40. Thus, the vast majority of linkage levels performed consistent with expectations for masters of the linkage levels.
Figure 5.1: Probability of Masters Providing a Correct Response to Items Measuring Each Linkage Level
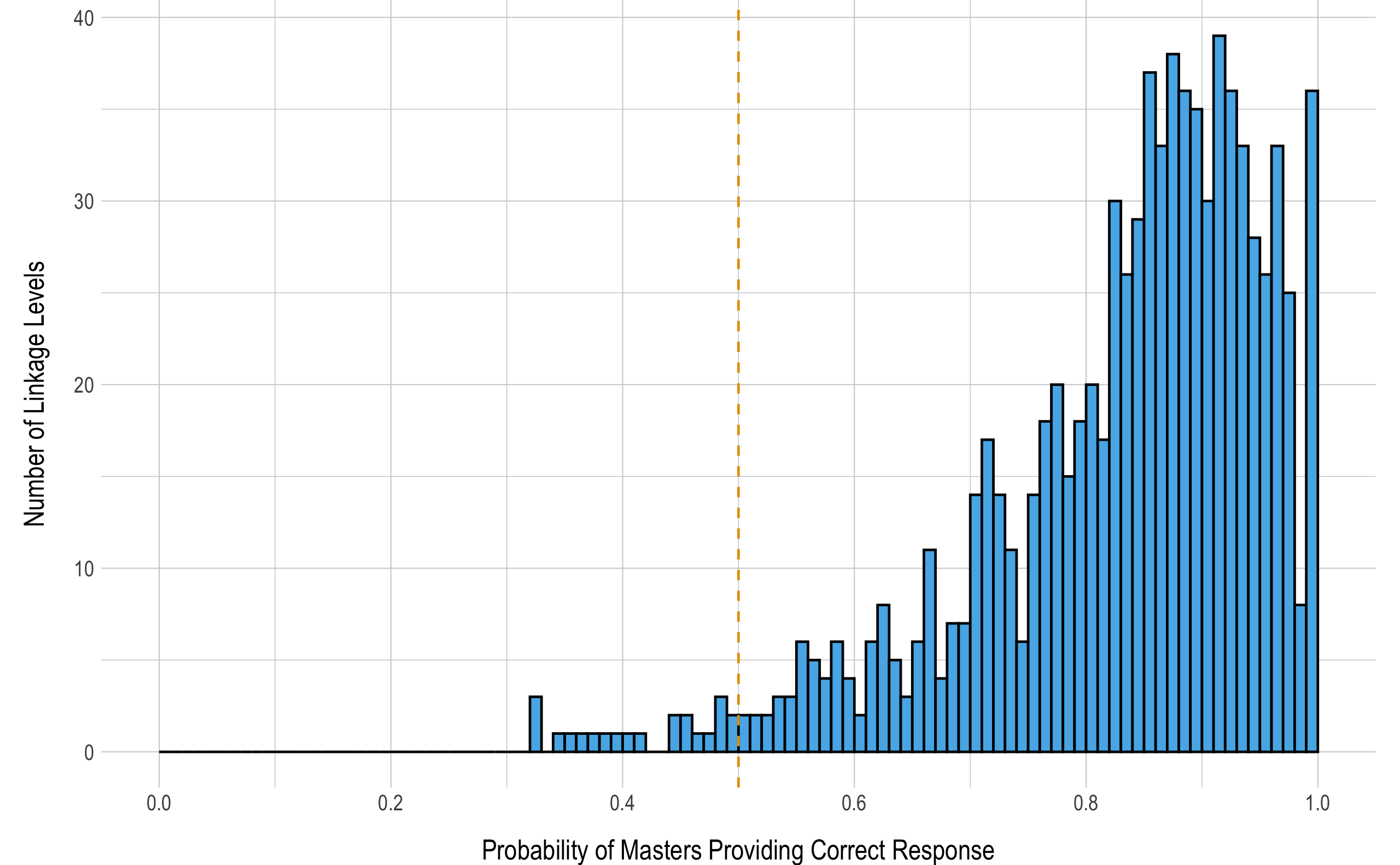
Note. Histogram bins are shown in increments of .01. Reference line indicates .50.
5.2.2 Probability of Non-Masters Providing Correct Response
When items measuring each linkage level function as expected, non-masters of the linkage level have a low probability of providing a correct response to items measuring the linkage level. Instances where non-masters have a high probability of providing correct responses may indicate that the linkage level does not measure what it is intended to measure, or that the correct answers to items measuring the level are easily guessed. These instances may result in students who have not mastered the content providing correct responses and being incorrectly classified as masters. This outcome has implications for the validity of inferences that can be made from results and for teachers using results to inform instructional planning in the subsequent year.
Figure 5.2 summarizes the probability of non-masters providing correct responses to items measuring each of the 860 linkage levels. There is greater variation in the probability of non-masters providing a correct response to items measuring each linkage level than was observed for masters, as shown in Figure 5.2. While the majority linkage levels (n = 722, 84%) performed as expected, non-masters sometimes had a greater than chance (> .50) likelihood of providing a correct response to items measuring the linkage level. Although most linkage levels (n = 548, 64%) have a conditional probability of non-masters providing a correct response less than .40, 53 (6%) have a conditional probability for non-masters providing a correct response greater than .60, indicating there are many linkage levels where non-masters are more likely than not to provide a correct response. This may indicate the items (and linkage level as a whole, since the item parameters are shared) were easily guessable or did not discriminate well between the two groups of students.
Figure 5.2: Probability of Non-masters Providing a Correct Response to Items Measuring Each Linkage Level
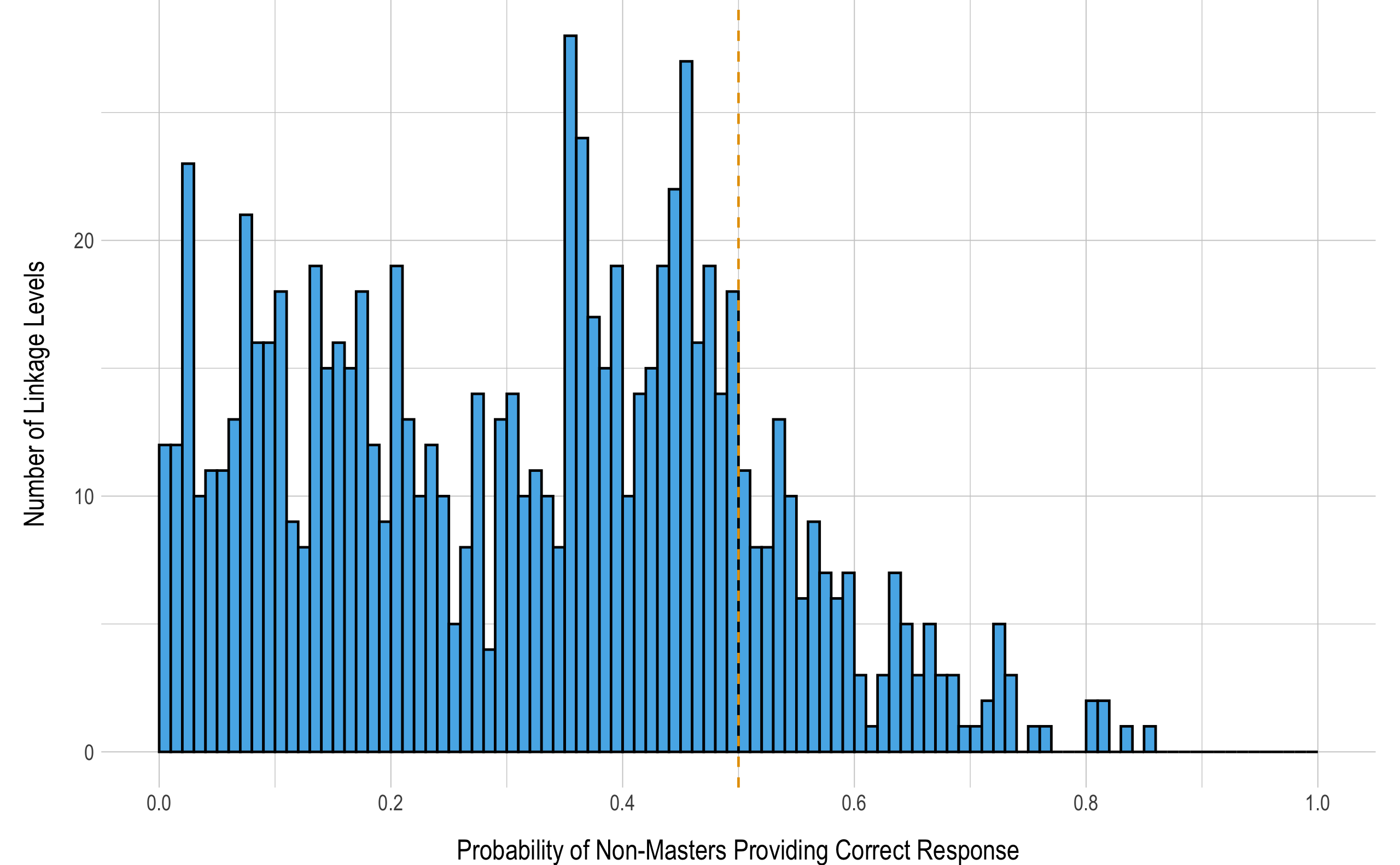
Note. Histogram bins are in increments of .01. Reference line indicates .50.
5.2.3 Item Discrimination
The discrimination of a linkage level represents how well the items are able to differentiate masters and non-masters. For diagnostic models, this is assessed by comparing the conditional probabilities of masters and non-masters providing a correct response. Linkage levels that are highly discriminating will have a large difference between the conditional probabilities, with a maximum value of 1.00 (i.e., masters have a 100% chance of providing a correct response and non-masters a 0% chance). Figure 5.3 shows the distribution of linkage level discrimination values. Overall, 73% of linkage levels (n = 628) have a discrimination greater than .40, indicating a large difference between the conditional probabilities (e.g., .75 to .35, .90 to .50, etc.). However, there were 12 linkage levels (1%) with a discrimination of less than .10, indicating that masters and non-masters tend to perform similarly on items measuring these linkage levels.
Figure 5.3: Difference Between Masters’ and Non-masters’ Probability of Providing a Correct Response to Items Measuring Each Linkage Level
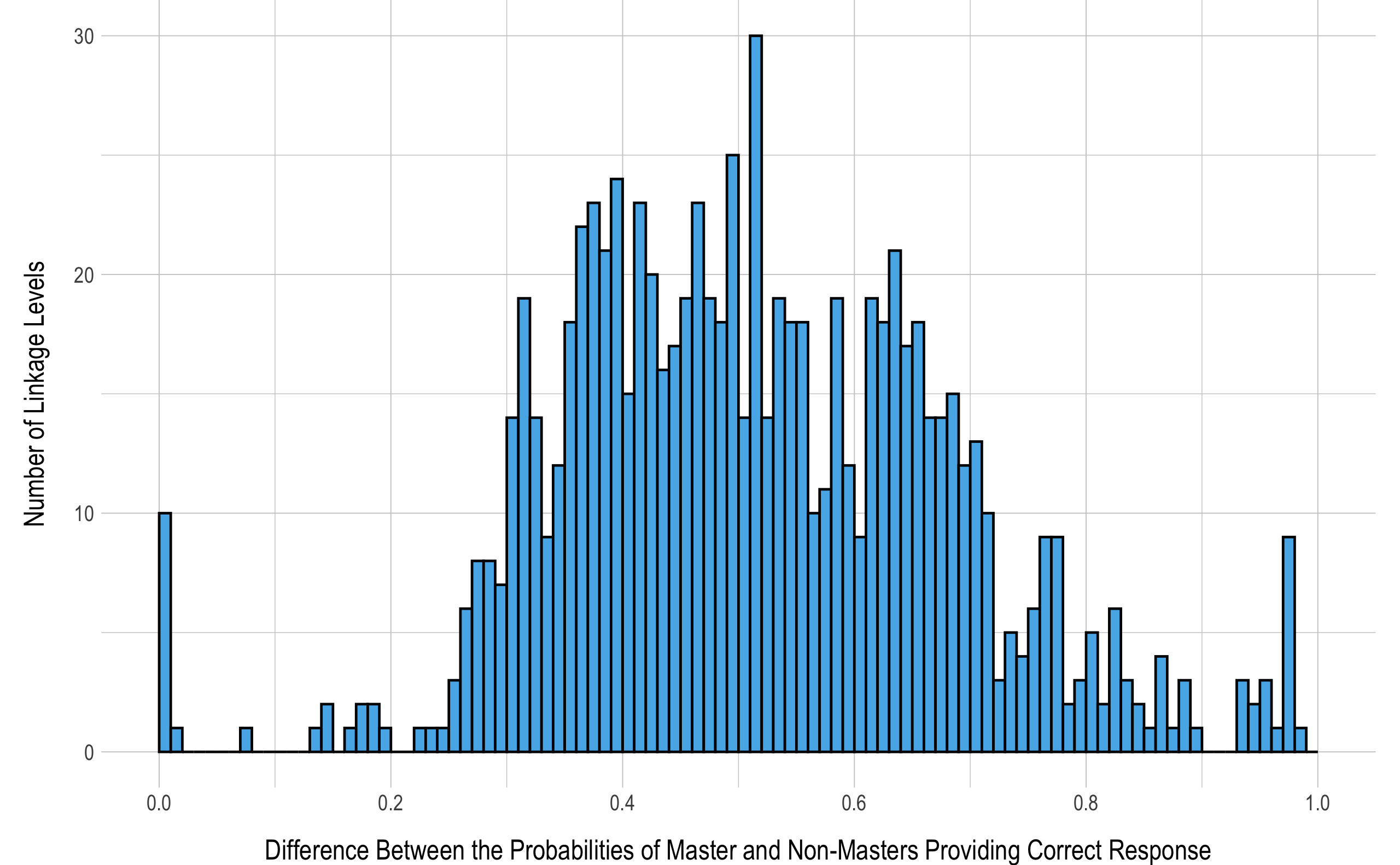
Note. Histogram bins are in increments of .01. Reference line indicates .50.
5.2.4 Base Rate Probability of Mastery
The DLM assessments are designed to maximize the match of student knowledge and skill to the appropriate linkage level content. The base rate of mastery represents the estimated proportion of masters among students assessed on an EE and linkage level. A base rate of mastery close to .50 indicates that students assessed on a given linkage level are equally likely to be a master or non-master. Conversely a high base rate of mastery would indicate that nearly all students testing on a linkage level are classified as masters. Figure 5.4 depicts the distribution of the base rate of mastery probabilities. Overall, 71% of linkage levels (n = 607) had a base rate of mastery between .25 and .75. This indicates that most linkage levels are performing as expected. On the edges of the distribution, 78 linkage levels (9%) had a base rate of mastery less than .25, and 175 linkage levels (20%) had a base rate of mastery higher than .75. This indicates that students are more likely to be assessed on linkage levels they have mastered than those they have not mastered.
Figure 5.4: Base Rate of Linkage Level Mastery
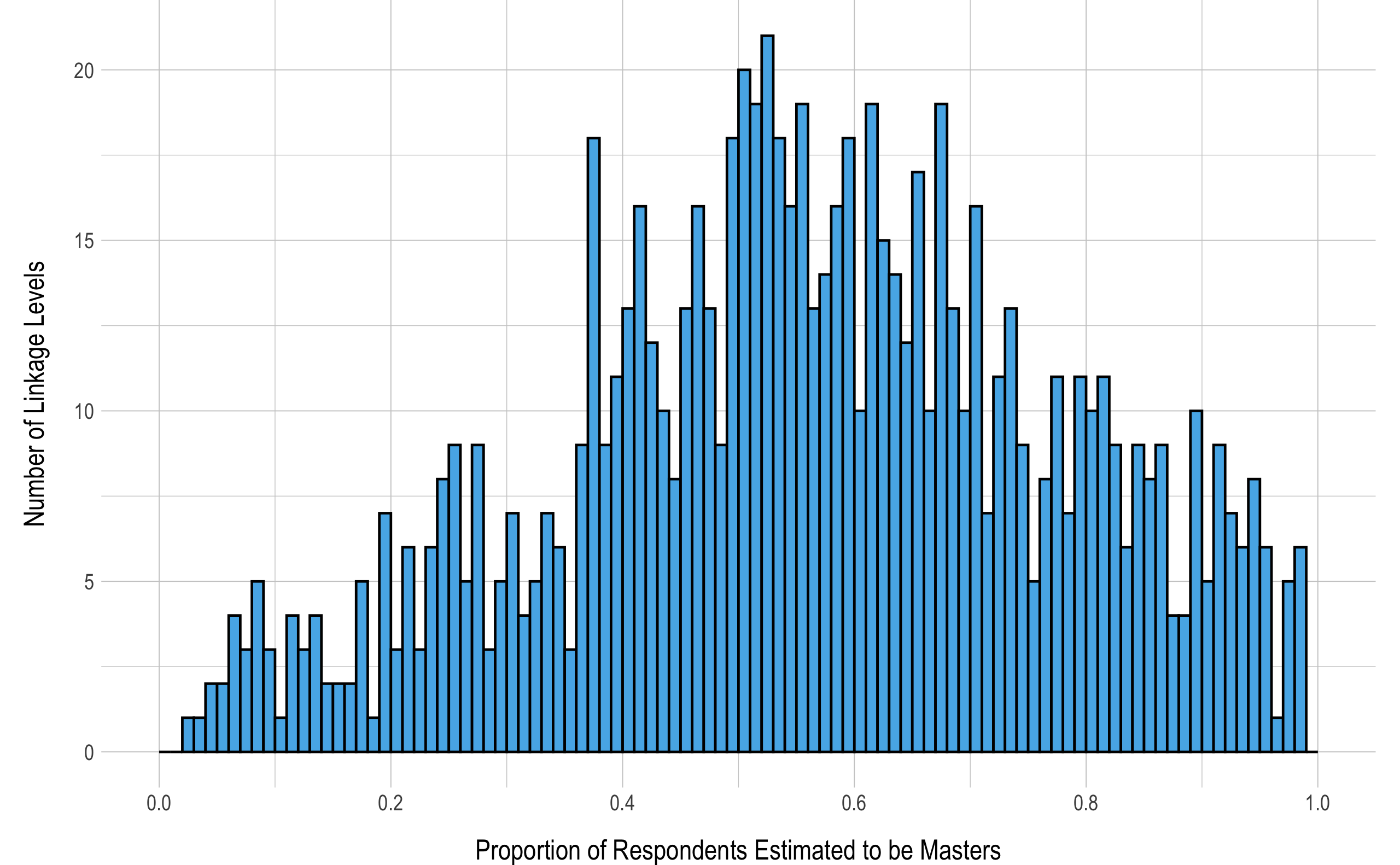
Note. Histogram bins are shown in increments of .01.
5.3 Mastery Assignment
Assessment administration during the 2019–2020 academic year was interrupted due to the COVID-19 pandemic. Due to school closures in response to the pandemic, very few students completed all assessments. Because very few students completed the assessment, the analysis of mastery assignment for 2019–2020 would be based on a limited sample that may not be representative of the full DLM population. Therefore, an updated analysis of mastery assignment is not provided for the 2019–2020 administration. Please refer to the Dynamic Learning Maps Consortium (2019b) for the most recent evidence of mastery assignment.
5.4 Model Fit
Model fit has important implications for the validity of inferences that can be made from assessment results. If the model used to calibrate and score the assessment does not fit the data well, results from the assessment may not accurately reflect what students know and can do. Relative and absolute model fit were compared following the 2017 administration. Model fit research was also prioritized during the 2017–2018, 2018–2019, and 2019–2020 operational years, and frequent feedback was provided by the DLM Technical Advisory Committee (TAC) modeling subcommittee, a subgroup of TAC members focused on reviewing modeling-specific research. During the 2018–2019 year, the modeling subcommittee reviewed research related to Bayesian methods for assessing model and item-level fit using posterior predictive model checks (Gelman et al., 1996; Gelman & Hill, 2006), the effect of partial equivalency constraints on model parameters, and new methods for model comparisons (e.g., Vehtari et al., 2017). For a summary of methods explored and their applicability to DLM assessments, see Thompson (2019).
For a complete description of the methods and process used to evaluate model fit, see Chapter 5 of the 2016–2017 Technical Manual Update—Year-End Model (Dynamic Learning Maps Consortium, 2017c).
5.5 Conclusion
In summary, the DLM modeling approach uses well-established research in Bayesian inference networks and diagnostic classification modeling to determine student mastery of skills measured by the assessment. Latent class analyses are conducted for each linkage level of each EE to determine the probability of student mastery. Items within the linkage level are assumed to be fungible, with equivalent item probability-parameters for masters and non-masters, owing to the conceptual approach used to construct DLM testlets. For each linkage level, a mastery threshold of .80 is applied, whereby students with a posterior probability greater than or equal to the threshold are deemed masters, and students with a posterior probability below the threshold are deemed non-masters. To ensure students are not excessively penalized by the modeling approach, in addition to posterior probabilities of mastery obtained from the model, two additional scoring procedures are implemented: percentage correct at the linkage level and a two-down scoring rule.